3496. Subset sums

For many sets of consecutive integers from 1 to n, one can partition it into two subsets with identical sums.

For example, if n = 3, one can partition the set {1, 2, 3} only in one way so that the sums of both subsets are identical:

· {3} and {1, 2}

This is considered as a single partitioning (reversing the order is considered as the same partitioning and thus does not increase the number of partitions).

If n = 7, there are four ways to partition the set {1, 2, 3, ..., 7} so that each partition has the same sum:

· {1, 6, 7} and {2, 3, 4, 5}

· {2, 5, 7} and {1, 3, 4, 6}

· {3, 4, 7} and {1, 2, 5, 6}

· {1, 2, 4, 7} and {3, 5, 6}

Given the value of n, print the number of ways a set of all integers from 1 to n can be partitioned into two subsets with equal sums. Print 0 if there are no such ways.

Input. One integer n (1 ≤ n ≤ 39).

Output. Print the number of same – sum partitions that can be made from the set {1, 2, ..., n}. Print 0 if the partition does not exist.

Sample input	Sample output
7	4

SOLUTION

dynamic programming

Algorithm analysis

Let s be the sum of all integers from 1 to n. If s is odd, then the answer is 0. Otherwise, the answer equals to the number of ways in which a subset with the sum of elements s / 2 can be chosen, divided by 2. The latter should be done so that the partitions A È B and B È A are considered the same.

Let m[s] contains the number of ways in which a subset with sum s can be selected from the set {1, 2, ..., n}. Initially set m[0] = 1.

Let the array m be already filled in the required way for numbers from the set {1, 2, ..., i – 1}. The next number i comes. Then m[j – i] should be added to any value of m[j] (i ≤ j < MAX).

Example

Let n = 7. The sum of all numbers from 1 to 7 is (1 + 7) / 2 * 7 = 28. Let’s find the number of ways to construct a subset with the sum of elements 14.

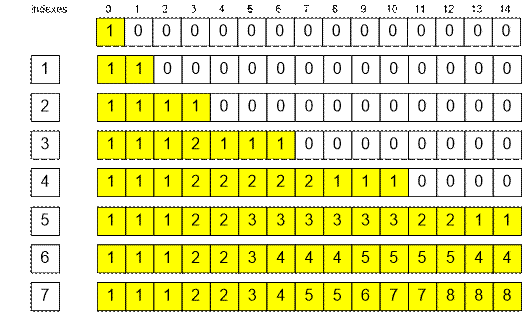
After processing the set {1, 2}, we have the following state of the array:

· m[0] = 1: the sum 0 is represented with an empty subset;

· m[1] = 1: the sum 1 is represented with subset {1};

· m[2] = 1: the sum 2 is represented with subset {2};

· m[3] = 1: the sum 3 is represented with subset {1, 2};

The next element of the set i = 3 arrives. To any value m[j] (3 ≤ j < MAX) one should add m[j – 3]. Non-zero values of m[j] will be the following:

· m[6] = m[6] + m[3] = 0 + 1 = 1, subset {1, 2, 3};

· m[5] = m[5] + m[2] = 0 + 1 = 1, subset {2, 3};

· m[4] = m[4] + m[1] = 0 + 1 = 1, subset {1, 3};

· m[3] = m[3] + m[0] = 1 + 1 = 2, subsets {1, 2}, {3};

Algorithm realization

Declare the array.

#define MAX 1001

long long m[MAX];

Read the value of n.

scanf("%lld",&n);

Initialize and fill array m.

memset(m,0,sizeof(m)); m[0] = 1;

for(i = 1; i <= n; i++)

for(j = MAX - 1; j >= i; j--) m[j] += m[j - i];

Find the sum of numbers from 1 to n. Print the result.

s = (1 + n) * n / 2;

if (s % 2 == 1) printf("0\n");

else printf("%lld\n",m[s/2]/2);